NCERT Solutions class 10 maths chapter 11
Constructions
NCERT Solutions class 10 maths chapter 11 Exercise 11.2
Question 1
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.Answer
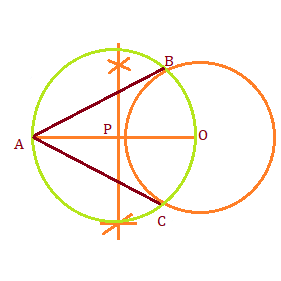
Step 1:Draw a circle of radius 6cm
Step 2:Make point outside of circle say 'A' such that AO is 10cm
Step 3:Make a perpendicular bisector of AB .P is mid point of AB
Step 4:P as center ,Draw a circle such that it intersect the previous circle at point B and C
Step 5:Join AB and AC
Step 6:AB and AC are the required tangents.
Question 2
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.Answer
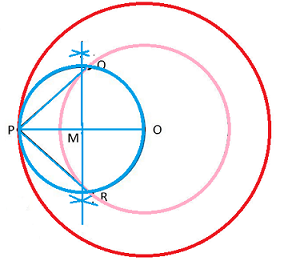
Step 1: Draw a circle of radius 6 cm with centre 'O'.
Step 2: Again, 'O' as centre draw a circle of radius 4 cm
Step 3:Make a point P on outer circle such that line PO
Step 4:Draw the perpendicular bisector of line OP and M be the mid point of PO.
Step 5:M as center ,Draw a circle such that it intersect the previous circle at point Q and R
Step 6:Join PQ and PR.
Step 7:PQ and PR are the tangents of circle
Question 3
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.Answer
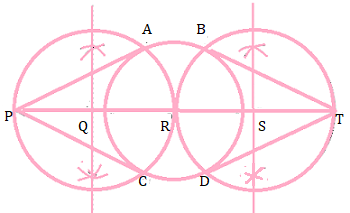
Step 1:Draw a circle of radius 3cm with centre 'R'.
Step 2: Produce a diameter of a circle and extends 7 cm at both end and mark point P and T.
Step 3: Draw the perpendicular bisector of the line PR and RT and Q midpoint of PR and S is midpoint of RT.
Step 4: Q as centre ,Draw a circle intersects the circle at A and C
Step 5:Again S as centre ,Draw a circle intersects the circle at B and D
Step 6: join PA and PC .
Step 7: PA and PC are the tangents.
Step 8: Also TB and TD are tangents.
Question 4
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°Answer
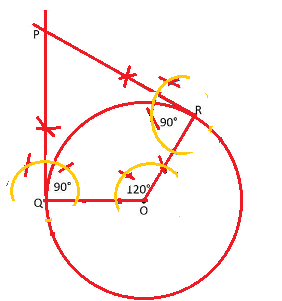
Step 1:Draw a circle of radius 5 cm with centre as O.
Step 2: Take a point Q on the circle and join OQ.
Step 3: Draw a radius OR, angle of 120° with OQ.
Step 4: At point Q and R draw angle 90.
Step 5: Now both the perpendiculars intersect at point P.
Step 6: PQ and PR are the tangents at an angle of 60°
Question 5
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.Answer
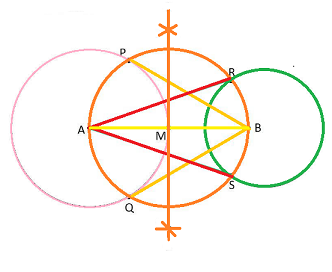
Step 1:Draw a line AB = 8 cm.
Step 2:Take A as centre draw a circle of radius 4 cm
Step 3: Similarly B as centre, draw a circle of radius 3 cm
Step 4: Draw the perpendicular bisector of the line AB with M midpoint .
Step 5: M as centre draw a circle with the radius of MA the intersects the circle at the points P, Q, R and S.
Step 6: Now join AR, AS, BP and BQ
Step 7: The tangents are AR, AS, BP and BQ
Question 6
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠ B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.Answer
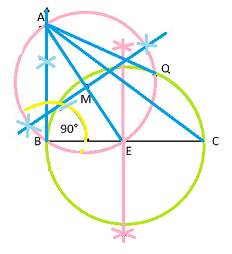
Step 1: Draw the line BC of 8cm
Step 2: make angle 'B' is 90°.
Step 3: Take 'B' as centre and draw an arc with a of 6cm.
Step 4: 'A' is point where the arc intersects the line and Join the line AC
Step 5: ABC be the required triangle.
Step 6: draw the perpendicular bisector of line BC with 'E' as a midpoint .
Step 7: 'E' as centre draw a circle.And Join 'A' to the midpoint E of the circle
Step 8: draw the perpendicular bisector to the line AE With M as a midpoint
Step 9: Take M as Centre , draw a circle.
Step 10: circle intersects the previous circle at the points B and Q
Step 11: Join the points AB and AQ
Step 12: AB and AQ are the required tangents
Question 7
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.Answer
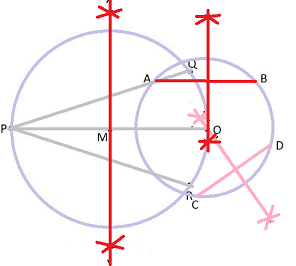
Step 1: Draw a circle with two chords such as AB and CD
Step 2: Draw the perpendicular bisector of AB and CD
Step 3: 'O' as a centre with the perpendicular bisector intersects.
Step 4: take a point 'P' outside the circle.
Step 5: Join the points 'O' and 'P'.
Step 6: Draw the perpendicular bisector of the line PO with 'M' midpoint
Step 7: 'M' as centre a draw a circle.
Step 8: Circle intersects at the points 'Q' and 'R'
Step 9: Now join PQ and PR
Step 10: PQ and PR are the required tangents.