NCERT Solutions class 10 maths chapter 8

Introduction to Trigonometry

NCERT Solutions class 10 maths chapter 8 Exercise 8.1

Question 1

In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C

Answer

In a given triangle ABC,
∠B = 90°
Given: AB = 24 cm and BC = 7 cm By applying Pythagoras theorem, we get
AC ²=AB ²+BC ²
AC ² = (24) ²+7 ²
AC ² = (576+49)
AC ² = 625cm ²
AC = √625 = 25
Therefore, AC = 25 cm
(i) Sin A, Cos A We know that Sin (A) = = =
Cos (A) = = =
(ii) Sin C, Cos C
Sin C = =
Cos C = =

Question 2

In Fig. 8.13, find tan P – cot R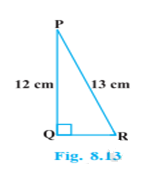

Answer

In the given triangle PQR,
PR = 13cm, PQ = 12cm
apply the Pythagorean theorem
PR² = QR² + PQ²
13² = QR² +12²
169 = QR² + 144
QR² = 169−144
QR² = 25
QR = √25 = 5
Therefore, the side QR = 5 cm
So tan P – cot R:
tan P = = =
Cot R = = =
Therefore, tan P – cot R = – = 0
Therefore, tan P – cot R = 0

Question 3

If sin A = , Calculate cos A and tan A.

Answer

Let a right angled triangle ABC, right angled at B
Given: Sin A =
Therefore, Sin A = =
Let BC be 3k and AC be 4k
where k is a positive real number.
AC²=AB² + BC²
(4k)²=AB² + (3k)²
16k² − 9k² =AB²
AB² = 7k²
Therefore, AB = √7k
Cos A = = =
Therefore, cos A =
tan A = = = =
Therefore, tan A =

Question 4

Given 15 cot A = 8, find sin A and sec A.

Answer

Let us assume a right angled triangle ABC, right angled at B
Given: 15 cot A = 8
So, Cot A =
Therefore, cot A = = =
Let AB be 8k and BC be 15k
Where, k is a positive real number.
According to the Pythagoras theorem,
AC₂=AB₂ + BC₂
AC₂= (8k)₂ + (15k)₂
AC₂= 64k₂ + 225k₂
AC₂= 289k₂
Therefore, AC = 17k
We know that,
Sin A =
Sin A = = =
Therefore, sin A =
Sec A =
we get,
= =
Therefore sec A =

Question 5

Given sec θ = Calculate all other trigonometric ratios

Answer

Let us assume a right angled triangle ABC, right angled at B
sec θ = = =
Let AC be 13k and AB be 12k
Where, k is a positive real number.
According to the Pythagoras theorem,
AC²=AB² + BC²
(13k)²= (12k)² + BC²
169k²= 144k² + BC²
169k²= 144k² + BC²
BC² = 169k² – 144k²
BC²= 25k²
Therefore, BC = 5k
Sin θ = = =
Cos θ = = =
tan θ = = =
Cosec θ = = =
cot θ = = =

Question 6

If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠ A = ∠ B.

Answer

Let us assume the triangle ABC in which CD⊥AB
Give that the angles A and B are acute angles, such that
Cos A = cos B
Cos =
Now, interchange the terms, we get
=
Let take a constant value
= = k
Now consider the equation as
AD = k BD …(1)
AC = k BC …(2)
By applying Pythagoras theorem in △CAD and △CBD we get,
CD² = BC² – BD² … (3)
CD² =AC² −AD² ….(4)
From the equations (3) and (4) we get,
AC² −AD² = BC² −BD²
Now substitute the equations (1) and (2) in (3) and (4)
K2(BC² − BD² )=(BC ²−BD²) k²=1
Putting this value in equation, we obtain
AC = BC
∠A=∠B (Angles opposite to equal side are equal-isosceles triangle)

Question 7

. If cot θ = 7/8, evaluate :
(i)
(ii) cot2 θ

Answer

Let us assume a △ABC in which ∠B = 90° and ∠C = θ
Given: cot θ = BC/AB = 7/8
Let BC = 7k and AB = 8k, where k is a positive real number
According to Pythagoras theorem in △ABC we get.
AC ² = AB²+BC²
AC² = (8k)²+(7k)²
AC² = 64k²+49k²
AC² = 113k²
AC = √113 k
sin θ = AB/AC = Opposite Side/Hypotenuse
= 8k/√113 k = 8/√113 and
cos θ = Adjacent Side/Hypotenuse
= BC/AC = 7k/√113 k = 7/√113

Question 8

If 3 cot A = 4, check whether (1-tan2 A)/(1+tan2 A) = cos2 A – sin 2 A or not.
sssss

Answer

Let △ABC in which ∠B=90°
cot(A) = AB/BC = 4/3
Let AB = 4k an BC =3k, where k is a positive real number.
According to the Pythagorean theorem,
AC²=AB²+BC²
AC²=(4k)²+(3k)²
AC²=16k²+9k²
AC²=25k²
AC=5k
tan(A) = BC/AB = 3/4
sin (A) = BC/AC = 3/5
cos (A) = AB/AC = 4/5
Now compare the left hand side(LHS) with right hand side(RHS)
Since, both the LHS and RHS = 7/25
R.H.S. =L.H.S.
Hence, = cos2 A – sin 2 A is proved

Question 9

. In triangle ABC, right-angled at B, if tan A = 1/√3 find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C

Answer

Let ΔABC in which ∠B=90°
tan A = BC/AB = 1/√3
Let BC = 1k and AB = √3 k,
Where k is the positive real number of the problem
By Pythagoras theorem in ΔABC we get:
AC²=AB²+BC²
AC²=(√3 k)2² + (k)²
AC²=3k²+k²
AC²=4k²
AC = 2k
Sin A = BC/AC = 1/2
Cos A = AB/AC = √3/2
Sin C = AB/AC = √3/2
Cos C = BC/AC = 1/2
Now, substitute the values in the given problem
(i) sin A cos C + cos A sin C
= (1/2) ×(1/2 )+ √3/2 ×√3/2 = 1/4 + 3/4 = 1
(ii) cos A cos C – sin A sin C
= (√3/2 )(1/2) – (1/2) (√3/2 ) = 0

Question 10

In ∆ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P
Solution:
In a given triangle PQR
PQ = 5 cm
PR + QR = 25 cm
Now let us assume, QR = x
PR = 25-QR
PR = 25- x
According to the Pythagorean Theorem,
PR2 = PQ2 + QR2
Substitute the value of PR as x
(25- x) ² = 5² + x²
25² + x – 50x = 25 + x²
625 + x²-50x -25 – x² = 0
-50x = -600
x= -600/-50
x = 12 = QR
Now, find the value of PR
PR = 25- QR
Substitute the value of QR
PR = 25-12
PR = 13
Now, substitute the value to the given problem
(1) sin p = Opposite Side/Hypotenuse
= QR/PR = 12/13
(2) Cos p = Adjacent Side/Hypotenuse
= PQ/PR = 5/13
(3) tan p =Opposite Side/Adjacent side
= QR/PQ = 12/5
11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 12/5 for some value of angle A.
(iii)cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = 4/3 for some angle θ.

Answer

(i) The value of tan A is always less than 1.

Answer

: False
Proof: In ΔMNC in which ∠N = 90∘,
MN = 3, NC = 4 and MC = 5
tan M = 4/3.
Pythagoras theorem.
MC²=MN2+NC²
52<< /sup>=3²+4²
25=9+16
25 = 25
(ii) sec A = 12/5 for some value of angle A

Answer

: True
Justification: Let a ΔMNC in which ∠N = 90º,
MC=12k and MB=5k, where k is a positive real number.
By Pythagoras theorem we get,
MC²=MN²+NC²
(12k)²=(5k)²+NC²
NC²+25k²=144k²
NC²=119k²
Such a triangle is possible as it will follow the Pythagoras theorem.
(iii) cos A is the abbreviation used for the cosecant of angle A.

Answer

: False
Justification: Abbreviation used for cosecant of angle M is cosec M. cos M is the abbreviation used for cosine of angle M.
(iv) cot A is the product of cot and A.

Answer

: False
Justification: cot M is not the product of cot and M. It is the cotangent of ∠M.
(v) sin θ = 4/3 for some angle θ.

Answer

: False
Justification: sin θ = Height/Hypotenuse
We know that in a right angled triangle, Hypotenuse is the longest side.
∴ sin θ will always less than 1 and it can never be 4/3 for any value of θ.

Exercise 8.2 Exercise 8.3 Exercise 8.4