Quick actions
Stay organised
Bookmark tricky proofs or add doubts to your dashboard so they resurface before exams.
Open dashboard →NCERT Solutions for Class 10 Maths Chapter 7 – Coordinate Geometry
Master "Coordinate Geometry" with step-by-step NCERT solutions.
Exercise 7.2
Answer
Let P(x, y) be the required point.the section formula x=ssand y=
So x1 = -1 , x2 =4 ,y1=7 ,y2= -3
and m1 = 2 , m2 =3
so
x =
y =
the point is (1, 3)
Question 2
. Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).Answer
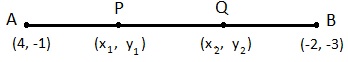
. Here Let assume P (x1, y1) and Q(x2, y22) are the points of trisection so AP = PQ = QB 1:2. here we know
x =
y =
x1 =
= (-2+8)/3 = 6/3 = 2
y1 =
= (-3-2)/3 = -5/3
Therefore: P (x1, y1) = P(2, -5/3) Point Q divides AB internally in the ratio 2:1. x2 =
= (-4+4)/3 = 0
y2 =
= (-6-1)/3 = -7/3
The coordinates of the point Q is (0, -7/3)
Question 3
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in the following figure. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?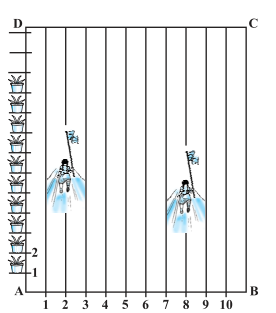
.
Answer
we observed that Niharika posted the green flag at 1/4th of the distance AD i.e., (1/4 ×100) m = 25m from the starting point of 2nd line. Therefore, the coordinates of this point are (2, 25).Similarly, Preet posted red flag at 1/5 of the distance AD i.e., (1/5 ×100) m = 20m from the starting point of 8th line. Therefore, the coordinates of this point are (8, 20).
Distance between these flags
. The point at which Rashmi should post her blue flag is the mid- point of the line joining these points. Let say this point be B(x, y).
x = (2+8)/2 = 10/2 = 5
y = (20+25)/2 = 45/2
B( x, y) = (5,45/2)
Therefore, Rashmi should post her blue flag at 45/2 = 22.5m on 5th line.
Question 4
Find the ratio in which the line segment joining the points (-3, 10) and (6, – 8) is divided by (-1, 6).Answer
Let assume the ratio in which the line segment joining ( -3, 10) and (6, -8) is divided by point ( -1, 6) be k :1.
So , -1 =
–k – 1 = 6k -3
7k = 2
k = 2/7
Therefore, the required ratio is 2:7.
Question 5
Find the ratio in which the line segment joining A (1, – 5) and B (- 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.Answer
Let the ratio in which the line segment joining A (1, – 5) and B ( – 4, 5) is divided by x-axis be k : 1.
Therefore, the coordinates of the point of division, say Q(x, y) is
We know that y-coordinate of any point on x-axis is 0.
Therefore,
5k = 5
or k = 1
So, x-axis divides the line segment in the ratio 1:1.
the point of division:
Q (x, y) =
=
Question 6
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.Answer
Let A,B,C and D be the vertex of a parallelogram : A(1,2), B(4,y), C(x,6) and D(3,5). and O is intersection point of diagonal AC and BD
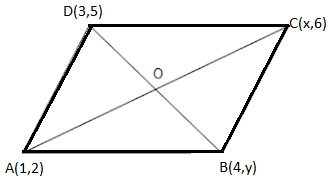
.
Since O is the midpoint of AC and BD .
Midpoint of AC
= ( (1+x)/2 , (2+6)/2 ) = ((1+x)/2 , 4)
Midpoint of BD
= ((4+3)/2 , (5+y)/2 ) = (7/2 , (5+y)/2)
Midpoint of AC and BD are same
(1+x)/2 = 7/2 and 4 = (5+y)/2
x + 1 = 7 and 5 + y = 8
x = 6 and y = 3.
Question 7
Find the coordinates of a point A, where AB is the diameter of circle whose centre is (2, – 3) and B is (1,4).Answer
Let the coordinates of point A be (x, y).
Mid-point of AB is (2, – 3), which is the centre of the circle.
Coordinate of B = (1, 4)
(2, -3) =((x+1)/2 , (y+4)/2)
(x+1)/2 = 2 and (y+4)/2 = -3
x + 1 = 4 and y + 4 = -6
x = 3 and y = -10
The coordinates of A(3,-10).
Question 8
If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that AP = 3/7 AB and P lies on the line segment AB.Answer

.
The coordinates of point A and B are (-2,-2) and (2,-4) respectively. Since AP = 3/7 AB
Therefore, AP: PB = 3:4
Point P divides the line segment AB in the ratio 3:4.
cordinate of P =
=
=
Question 9
Find the coordinates of the points which divide the line segment joining A (- 2, 2) and B (2, 8) into four equal parts.Answer
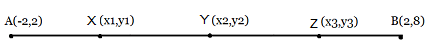
.
From the figure, it can be observed that points X, Y, Z are dividing the line segment in a ratio 1:3, 1:1, 3:1 respectively.
Cordinate of X =
= - 1 ,
cordinate of Y =
= (0 ,5 )
Cordinate of Z =
= - 1 ,
Question 10
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2,-1) taken in order.[Hint: Area of a rhombus = 1/2(product of its diagonals)
Answer
Let A(3, 0), B (4, 5), C( – 1, 4) and D ( – 2, – 1) are the vertices of a rhombus ABCD.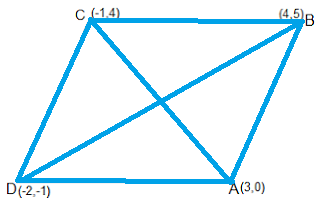
.
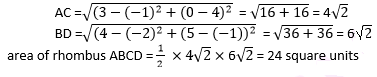
.
Chapter shortcuts
- Chapter 1 · Real Numbers
- Chapter 2 · Polynomials
- Chapter 3 · Pair of Linear Equations in Two Variables
- Chapter 4 · Quadratic Equations
- Chapter 5 · Arithmetic Progressions
- Chapter 6 · Triangles
- Chapter 7 · Coordinate Geometry
- Chapter 8 · Introduction to Trigonometry
- Chapter 9 · Some Applications of Trigonometry
- Chapter 10 · Circles
- Chapter 11 · Constructions
- Chapter 12 · Area Related to Circles
- Chapter 13 · Surface Areas and Volumes
- Chapter 14 · Statistics
- Chapter 15 · Probability