NCERT Solutions for class 10 maths chapter 2

Polynomials

NCERT Solutions for class 10 maths chapter 2 Exercise 2.2

Question 1

Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.

(i) x²–2x –8

(ii) 4s²–4s+1

(iii) 6x²–3–7x

(iv) 4u²+8u

(v) t²–15

(vi) 3x²–x–4

Answer

(i) x²–2x –8

⇒x²– 4x+2x–8
= x(x–4)+2(x–4)
= (x-4)(x+2)

here zeroes of polynomial equation
x-4 =0
x=4
x+2=0
x=-2

verification:

hence verify

(ii) 4s²–4s+1

Answer

⇒4s²–2s–2s+1
= 2s(2s–1)–1(2s-1)
= (2s–1)(2s–1)

Therefore, zeroes of polynomial equation
2s-1= 0
s=1/2
2s-1 =0
s=1/2

verification:

hence verify

(iii) 6x²–3–7x

Answer

⇒6x²–7x–3
= 6x² – 9x + 2x – 3 = 3x(2x – 3) +1(2x – 3)
= (3x+1)(2x-3)

Here , zeroes of polynomial equation
2x-3=0
x= -1/3
2x-3=0
s= 3/2

verification:

=

= x = =
=

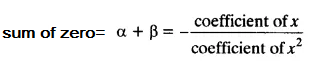
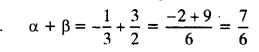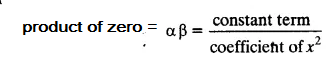
hence verify

(iv) 4u²+8u

Answer

⇒ 4u(u+2)

Here zeroes of polynomial equation
4u=0
u=0
u+2=0
u= -2.

verification:

=

hence verify

(v) t²–15

Answer

⇒ t² = 15 or t = ±√15

verification:

hence verify

here , zeroes of polynomial are (√15, -√15)

(vi) 3x²–x–4

⇒ 3x²–4x+3x–4
= x(3x-4)+1(3x-4)
= (3x – 4)(x + 1)

Therefore, zeroes of polynomial equation 3x-4 =0
x=4/3
x+ 1=0
x= -1)

verification:

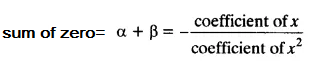
hence verify

Question 2

Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.

(i) 1/4 , -1

(ii)√2, 1/3

(iii) 0, √5

(iv) 1, 1

(v) -1/4, 1/4

(vi) 4, 1

Answer

(i) 1/4 , -1

From the formulas of sum and product of zeroes, we know,

Sum of zeroes = α+β = 1/4

Product of zeroes = α β = -1

We know that

x²–(α+β)x +αβ = 0

x²–(1/4)x +(-1) = 0

4x²–x-4 = 0

Thus,4x²–x–4

(ii)√2, 1/3

Answer

Sum of zeroes = α + β =√2

Product of zeroes = α β = 1/3

We know that

x²–(α+β)x +αβ = 0

x² –(√2)x + (1/3) = 0

3x²-3√2x+1 = 0

Thus, 3x²-3√2x+1

(iii) 0, √5

Answer

Sum of zeroes = α+β = 0

Product of zeroes = α β = √5

x²–(α+β)x +αβ = 0

x²–(0)x +√5= 0

Thus, x²+ √5 is the quadratic polynomial.

(iv) 1, 1

Answer

Given,

Sum of zeroes = α+β = 1

Product of zeroes = α β = 1

x²–(α+β)x +αβ = 0

x²–x+1 = 0

Thus , x²–x+1

(v) -1/4, 1/4

Answer

Given,

Sum of zeroes = α+β = -1/4

Product of zeroes = α β = 1/4

x²–(α+β)x +αβ = 0

x²–(-1/4)x +(1/4) = 0

>4x²+x+1 = 0

Thus,4x²+x+1

(vi) 4, 1

Answer

Given,

Sum of zeroes = α+β =

Product of zeroes = αβ = 1

x²–(α+β)x+αβ = 0

x²–4x+1 = 0

Thus, x²–4x+1