NCERT Solutions class 10 maths chapter 13

Surface Areas and Volumes

NCERT Solutions class 10 maths chapter 13 Exercise 13.3

Exercise 13.1 Exercise 13.2 Exercise 13.4 Exercise 13.5

Question 1

. A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.

Answer 1

radius of the sphere R = 4.2 cm

Radius of cylinder r = 6 cm

let height of cylinder = h

According to question

So, Volume of Sphere = Volume of Cylinder

∴ (4/3)×π×R³= π×r²×h.

h = 2.74 cm

Question 2

. Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.

Answer 2

For Sphere 1

Radius r₁ = 6 cm

∴ Volume V₁ = (4/3)×π×r₁³

For Sphere 2:

Radius r₂ = 8 cm

∴ Volume V₂ = (4/3)×π×r₂³

For Sphere 3:

Radius r₃ = 10 cm

∴ Volume V₃ = (4/3)× π× r₃³

the radius of the resulting sphere be R

Now,

Volume of resulting sphere = V₁+V₂+V₃

(4/3)×π×R³ = (4/3)×π×r₁³+(4/3)×π×r₂³ +(4/3)×π×r₃³

R³= 6³+8³+10³

R³= 1728

R = 12 cm

Question 3

. A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.

Answer 3

So, radius = 7/2 m

Also, height of deep well = 20 m

∴ Volume of Cylinder = π×r²×h

= 22×7×5 m³

Let the height of the platform = H

Volume of deep well (cylinder) = Volume of soil used to make such platform

π×r²×h = Area of platform × Height of the platform

We know that the dimension of the platform is = 22×14

So, Area of platform = 22×14 m²

∴ π×r²×h = 22×14×H

⇒ H = 2.5 m

Question 4

A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.

Answer 4

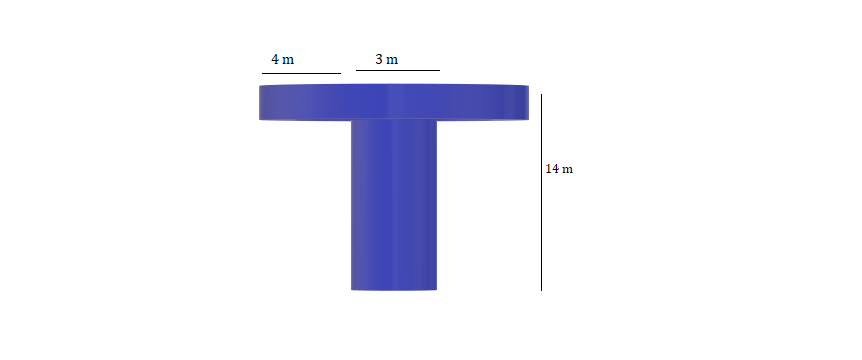
The shape of the well will be cylindrical as given below.

Depth (h₁) of well = 14 m

Diameter of the well =3 m

So, Radius r₁ = 3/2 m

Width of the embankment = 4 m

outer radius r₂ as 4 + (3/2) = 11/2 m and inner radius r₁ as 3/2 m

Now, let the height of embankment be h₂

∴ Volume of soil dug from well = Volume of earth used to form embankment

π×r₁²×h = π×(r₂²-r₁²) × h₂

(22/7) x (3/2)² x 14 = (22/7) x [(11/2)² - (3/2)²] x h₂

h₂ = (7 x 99 x 4 / 22 x 112) = 9/8 =1.125 m

The height of the embankment (h₂) as 1.125 m.

Question 5

A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.

Answer 5

For the cylinder

Radius = 12/2 = 6 cm

Height = 15 cm

∴ Volume of cylinder = π×r²×h = 540π

For the ice cone

Radius r = 6/2 = 3 cm

Height h = 12 cm

Radius of hemispherical = 6/2 = 3 cm

Now,

Volume of ice cream cone = Volume of conical + Volume of hemispherical

= (1/3)× π × r² × h+(2/3)× π × r³

= 36π +18π

= 54π

let n be the number of cone filed with ic-cream
Volume of cylinder = n x Volume of ice cream cone

∴ n = (540π/54π)

n=10

Question 6

How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?

Answer 6

we known that the coins are cylindrical in shape.

So, height h₁ of the cylinder = 2 mm = 0.2 cm

Radius r of circular end of coins = 1.75/2 = 0.875 cm

Now,let n be the number of coins to be melted to form the required cuboids/p>

Volume of n coins = Volume of cuboids

n × π × r²× h₁ = l × b × h

n×π×(0.875)²×0.2 = 5.5×10×3.5

Or, n = 400

Question 7

A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.

Answer 7

Given,

Height h₁ of the bucket = 32 cm

Radius r₁ of the bucket = 18 cm

Height of the conical heap h₂ = 24 cm

Now, let r be the radius of heap of sand .

According to question

∴ Volume of sand in the cylindrical bucket = Volume of sand in conical heap

π×r₁²×h₁ = (1/3)×π×r²×h₂

π×18²×32 = (⅓)×π × r²×24

Or, r = 36 cm

And,

Slant height l = √(36²+24²) = 12√13 cm.

Question 8

Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?

Answer 8

Breadth (b) = 6 m and Height (h) = 1.5 m

The speed of canal = 10 km/hr

Length of canal covered in 1 hour = 10 km

Length of canal covered in 60 minutes = 10 km

Length of canal covered in 1 min = (1/60)x10 km

Length of canal covered in 30 min (l) = (30/60)x10 = 5km = 5000 m

We know that the canal is cuboidal in shape. So,

Volume of canal = lxbxh

= 5000x6x1.5 m³

= 45000 m³

Now,

Volume of water in canal = Volume of area irrigated

= Area irrigated x Height

So, Area irrigated = 56.25 hectares

∴ Volume of canal = lxbxh

45000 = Area irrigatedx8 cm

45000 = Area irrigated x (8/100)m

Or, Area irrigated = 562500 m²= 56.25 hectares.

Question 9

A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?